0x00 前言
问题:实现一个 16M 大小的整数 int64 的数组排序,如何实现?采用多路归并方式实现
0x01 多路归并排序
先简单回顾下,多路归并排序(Multi-way merge sort)是归并排序的一种扩展,它可以同时合并多个有序数组。归并排序的基本思想是将两个有序数组合并成一个有序数组,而多路归并排序是将 k 个有序数组合并成一个有序数组。多路归并排序在处理大规模数据时,可以显著减少磁盘 I/O 次数,提高排序效率。多路归并排序的基本步骤如下:
- 将待排序的数据分为
k个有序数组 - 将
k个有序数组两两合并,得到k/2个有序数组。重复这个过程,直到剩下一个有序数组 - 输出合并后的有序数组
多路归并排序的时间复杂度为 O(nlogk),其中 n 是待排序数据的总数,k 是归并的路数。当 k=2 时,多路归并排序就是普通的归并排序。多路归并排序的实现可以使用优先队列(如 MinHeap)来选择每次合并的最小元素,从而提高合并的效率。具体步骤如下:
- 建立一个大小为
k的最小堆,将k个有序数组的首元素插入到堆中 - 每次从堆中取出最小元素,将其添加到合并后的数组中
- 将被取出元素所在数组的下一个元素插入堆中。如果该数组已经没有元素,就跳过这一步
- 重复步骤
2和3,直到堆为空
解决思路
- 将待排序数组分成多个组,利用多个 goroutine 实现各个组的并行排序;然后通过 MinHeap 进行多路归并排序
- 每个分组内直接调用
sort原生方法排序
代码分析
实现一个协程池实现任务的并行处理,将待排序切片分组并封装成 SortTask 放入协程池
运行,待全部执行完成后 ConcurrentSorter 收集排序结果,并封装成 MergeTask 放入协程池中进行合并。
1、排序算法 Sorter 、待排序(单个分组)的抽象定义为 SortableSlice,如下
type Sorter interface {
Sort()
GetSortable() SortableSlice
}
type SortableSlice interface {
Len() int
Less(i, j int) bool
Swap(i, j int)
Append(v int64)
IndexOf(int) (int64, error)
Pop() (int64, error)
GetSlice() []int64
}
Sorter 接口的实例化为 Quick,其对应初始化方法 NewQuick 传入的参数为 SortableSlice,SortableSlice 的实例化结构为 MinInt64Slice,定义如下:
type Quick struct {
slice SortableSlice
}
func NewQuick(p SortableSlice) *Quick {
return &Quick{slice: p}
}
type SortableSlice interface {
Len() int
Less(i, j int) bool
Swap(i, j int)
Append(v int64)
IndexOf(int) (int64, error)
Pop() (int64, error)
GetSlice() []int64
}
type MinInt64Slice struct {
array []int64 //
}
func (s *MinInt64Slice) GetSlice() []int64 {
return s.array
}
func (s *MinInt64Slice) Len() int {
return len(s.array)
}
func (s *MinInt64Slice) Less(i, j int) bool {
return s.array[i] < s.array[j]
}
func (s *MinInt64Slice) Swap(i, j int) {
s.array[i], s.array[j] = s.array[j], s.array[i]
}
func (s *MinInt64Slice) Append(v int64) {
s.array = append(s.array, v)
}
func (s *MinInt64Slice) IndexOf(i int) (int64, error) {
if len(s.array) > i {
return s.array[i], nil
}
return 0, errors.New("sorter is empty")
}
func (s *MinInt64Slice) Pop() (int64, error) {
if len(s.array) > 0 {
v := s.array[0]
s.array = s.array[1:]
return v, nil
}
return 0, errors.New("no element")
}
很明显,Quick 的主要作用就是对 Quick.slice 排序
2、通过 SortTask 启动单个分组的排序,然后将结果异步返回,从实现看,SortTask.Run() 必然要是并发执行的;为此,项目构建了一个并发协程池管理结构 ConcurrentSorter,用来完成分组的排序及结果输出
type SortTask struct {
sorter *algorithm.Quick
retChan chan *MinInt64Slice
}
func NewSortTask(src []int64, retChan chan *MinInt64Slice) *SortTask {
return &SortTask{
sorter: algorithm.NewQuick(&MinInt64Slice{
array: src,
}),
retChan: retChan,
}
}
// 在协程池调用此方法,进行排序和输出
func (s *SortTask) Run() error {
s.sorter.Sort()
// 运行结束返回结果
s.retChan <- s.sorter.GetSortable().(*MinInt64Slice)
return nil
}
type SortableSlice interface {
Len() int
Less(i, j int) bool
Swap(i, j int)
Append(v int64)
IndexOf(int) (int64, error)
Pop() (int64, error)
GetSlice() []int64
}
SortableSlice 的实例化结构为 MinInt64Slice,定义如下:
type MinInt64Slice struct {
array []int64 //
}
func (s *MinInt64Slice) GetSlice() []int64 {
return s.array
}
func (s *MinInt64Slice) Len() int {
return len(s.array)
}
func (s *MinInt64Slice) Less(i, j int) bool {
return s.array[i] < s.array[j]
}
func (s *MinInt64Slice) Swap(i, j int) {
s.array[i], s.array[j] = s.array[j], s.array[i]
}
func (s *MinInt64Slice) Append(v int64) {
s.array = append(s.array, v)
}
func (s *MinInt64Slice) IndexOf(i int) (int64, error) {
if len(s.array) > i {
return s.array[i], nil
}
return 0, errors.New("sorter is empty")
}
func (s *MinInt64Slice) Pop() (int64, error) {
if len(s.array) > 0 {
v := s.array[0]
s.array = s.array[1:]
return v, nil
}
return 0, errors.New("no element")
}
3、管理结构 ConcurrentSorter,用于拆分、组内并行排序 m.sort(),组件多路归并 m.merge(mergedChan),核心代码如下:
注意,在协程池中会调用 SortTask.Run() 方法进行排序和输出结果到 ConcurrentSorter.sortedChan
type ConcurrentSorter struct {
sortedChan chan *MinInt64Slice
sortingArray []int64
pool *pool.Pool
taskNum int
}
func NewConcurrent(src []int64) Sorter {
// 拆分成子任务并行完成
taskNum := runtime.NumCPU()
return &ConcurrentSorter{
sortedChan: make(chan *MinInt64Slice, 1),
sortingArray: src,
pool: pool.NewPool(&pool.Config{
QSize: 1,
Workers: runtime.NumCPU(),
MaxIdle: time.Second * 10,
}),
taskNum: taskNum,
}
}
func (m *ConcurrentSorter) sort() {
start := 0
step := len(m.sortingArray) / m.taskNum
// 不能整除,则最后一个 task 多处理一些
count := 1
for ; start <len(m.sortingArray); {
end := (start + step) % len(m.sortingArray)
// 最后一个任务
if m.taskNum == count {
end = len(m.sortingArray)
}
// 构建单个分组
t := NewSortTask(m.sortingArray[start:end], m.sortedChan)
start = end
// 将分组放入协程池排序
m.pool.Put(t)
count++
}
}
func (m *ConcurrentSorter) merge(mergedChan chan []int64) {
sortedSlices := make([][]int64, 0, m.taskNum)
sortedLen := 0
loop:
for {
select {
case s := <-m.sortedChan:
sortedLen += s.Len()
sortedSlices = append(sortedSlices, s.GetSlice())
// sort 阶段完成
if sortedLen == len(m.sortingArray) {
// 这里确保所有的 task 都已经退出,不然可能导致死锁
// 死锁产生的场景,SortTask.Run()->SortedChan, 如果该 routine 退出 <-m.sortedChan;
// 那么 SortedTask 无法退出;当前 task m.pool.Put(MergeTask) 就会阻塞
break loop
}
}
}
mergeTask := NewMergeTask(sortedSlices, mergedChan)
// 为避免死锁, 另外启动一个协程写入
m.pool.Put(mergeTask)
}
4、ConcurrentSorter 主入口
func (m *ConcurrentSorter) Run() {
mergedChan := make(chan []int64, 1)
defer func() {
m.pool.Close(true)
close(m.sortedChan)
close(mergedChan)
}()
wg := sync.WaitGroup{}
wg.Add(1)
go func() {
// 组间并行(排序)
m.sort()
wg.Done()
}()
wg.Add(1)
go func() {
// 归并
m.merge(mergedChan)
wg.Done()
}()
wg.Wait()
resultSlice := <-mergedChan
copy(m.sortingArray, resultSlice)
}
4、最后看看最核心的归并算法实现 m.merge(mergedChan)
- 输入:
n路待合并的有序 slice - 输出:有序 slice
堆 node 定义为一个 SortedSlice 结构,它实现了 HasNext 方法,用于迭代到当前 slice 的下一个元素
type SortedSlice struct {
slice []int64
Iterator
}
type Iterator struct {
slice []int64
index int
}
//
func (i *Iterator) HasNext() bool {
return i.index <len(i.slice)-1
}
func (i *Iterator) Next() {
i.index++
}
func (i *Iterator) Value() int64 {
return i.slice[i.index]
}
// 参数 slice 为有序数组
func NewSortedSlice(slice []int64) *SortedSlice {
return &SortedSlice{
slice: slice,
Iterator: Iterator{
slice: slice,
index: 0,
},
}
}
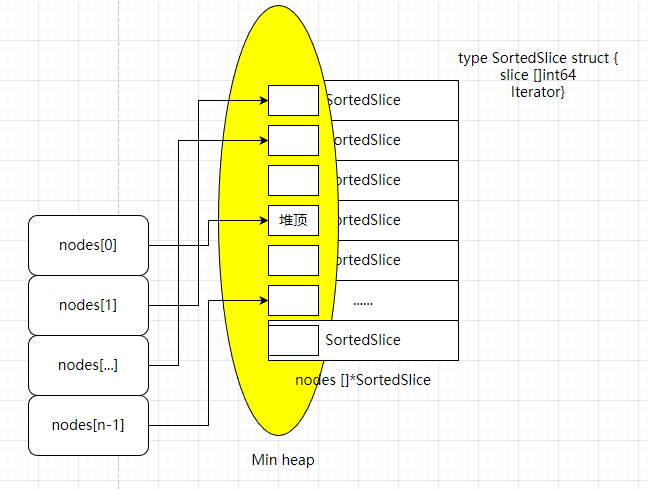
5、最小堆排序算法的实现
大致流程是,从每路 slice 中取首个元素组成数组,调整堆;每次从堆顶,取一个元素,放入合并后的 slice 中
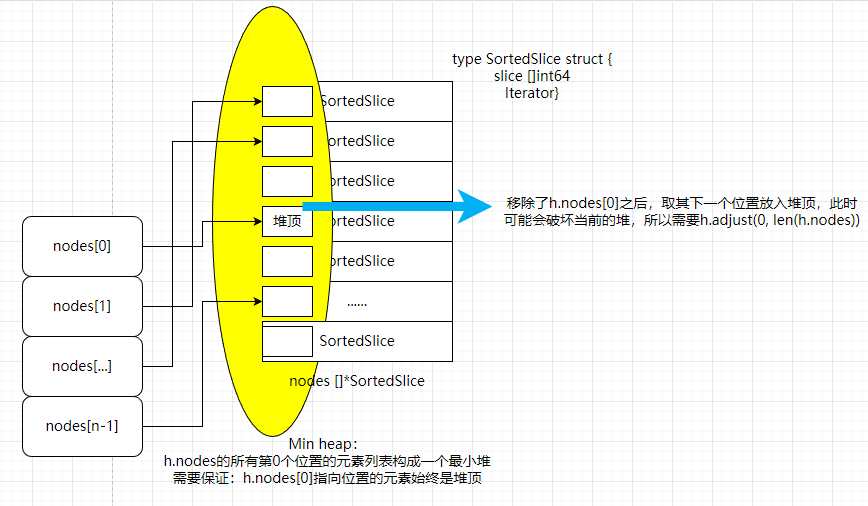
- 如果
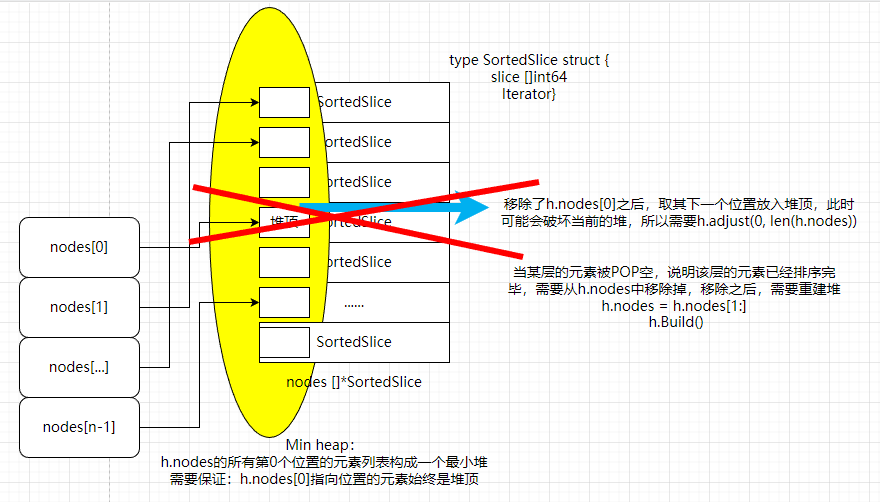
hasNext==true,执行当前 node 的Next(),重新调整当前的堆顶 - 如果
hasNext==false, 当前 slice 已经空了,因此剔除堆顶, 然后需要重建堆,原因是堆中的父子关系已经破坏
在多路归并实现中,若采用 2 路循环合并,每次合并需要申请长度为 2 路之和的内存保存合并结果,循环合并会导致过多的内存申请,通过最小堆实现多路的有序切片的合并,只需要额外申请一次 1 倍的内存用于存放合并结果即可
调用入口:
func (m *MergeTask) Run() error {
sortedSlices := make([]*algorithm.SortedSlice, 0, len(m.slices))
for _, s := range m.slices {
sortedSlices = append(sortedSlices, algorithm.NewSortedSlice(s))
}
merge := algorithm.NewHeapMerge(sortedSlices)
// 合并有序切片
m.retChan <- merge.Sort()
return nil
}
type HeapMerge struct {
nodes []*SortedSlice
}
// 构建一个 n 个元素的最小堆
func NewHeapMerge(sources []*SortedSlice) *HeapMerge {
// 需要保证
return &HeapMerge{nodes: sources}
}
func (h *HeapMerge) Build() {
for index := len(h.nodes) / 2; index >= 0; index-- {
h.adjust(index, len(h.nodes))
}
}
func (h *HeapMerge) Pop() (int64, error) {
var value int64
var err error
if len(h.nodes) > 0 {
value = h.nodes[0].Value() //从前面的步骤保证了,这里的value一定是最小值,Pop直接返回这个值;然后按照堆的性质调整堆即可
err = nil
if h.nodes[0].HasNext() {
h.nodes[0].Next() // 不需要获取值
// 取当前最小堆顶(即将被pop)的下一个位置元素,由于大概率会破坏堆的性质,所以需要调整堆(参考一般minheap的pop实现)
h.adjust(0, len(h.nodes))
} else {// 顶部的 node(slice) 已经为空
if len(h.nodes) >= 1 {
// 移除为已经合并完成的 slice
h.nodes = h.nodes[1:]
//h.adjust(0, len(h.nodes))
h.Build()
} else {
return 0, errors.New("merge complete")
}
}
} else {
return 0, errors.New("merge complete")
}
//h.Print()
return value, err
}
func (h *HeapMerge) adjust(start, end int) {
childIndex := 2*start + 1 //左边:2*start+1,右边:2*start+2(下标从0开始)
// 下标应该比长度小
if childIndex >= end {
// 递归退出的条件
return
}
if childIndex+1 <end && h.nodes[childIndex+1].Value() < h.nodes[childIndex].Value() {
// 如果start存在右边的孩子节点(childIndex+1 <end )
// 右孩子比左孩子的value小
childIndex++
}
//上面较小的节点,再和start位置比
if h.nodes[childIndex].Value() < h.nodes[start].Value() {
// 如果小,那么则需要交换start与childIndex这两个节点
h.nodes[start], h.nodes[childIndex] = h.nodes[childIndex], h.nodes[start]
// 一旦交换了之后,后面的节点要重新调整顺序
// 这里是采用递归的方法实现
h.adjust(childIndex, end)
}
}
// 入口
func (h *HeapMerge) Sort() []int64 {
h.Build()
length := 0
for _, c := range h.nodes {
length += len(c.slice)
}
mergeSlice := make([]int64, length, length)
mergeSliceIndex := 0
loop:
for {
v, err := h.Pop()
if err != nil {
break loop
} else {
// 替换掉 mergeSlice = append(mergeSlice,v) 节省了大约 10ms
mergeSlice[mergeSliceIndex] = v
//mergeSlice = append(mergeSlice, v)
}
mergeSliceIndex++
}
return mergeSlice
}
分析下Sort核心入口的实现:
首先,通过h.Build()进行初始化建堆,即对h.nodes([]*SortedSlice类型)的第一个位置的元素进行建立最小堆,最终h.Build()执行完成后,h.nodes[0].Value()这个位置的元素一定是最小的
用几张图汇总下上面的排序逻辑:
协程池的实现
- 配置最大协程数量
- 按需创建协程
- 空闲超时则回收协程